20.12.2019 | Matematika

Elipsa, geometrijska definicija

Vsi že vemo, kakšna je elipsa (kot kakšno jajce). Matematike pa nadvse navduši, če lahko eno in isto stvar opišejo na več načinov, tako so za elipso našli dva:

Enkrat jo opišejo kot množico točk, kjer vsota razdalj do dveh gorišč ne glede na točko konstantna. (To je takrat, kadar si nadenejo očala s trikotnimi okvirji, torej geometrijska definicija elipse.)

Drugič pa jo opišejo z enačbo.

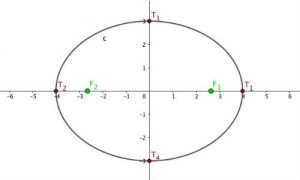
Geometrijsko definicijo elipse lahko zapišemo takole:
če je točka na elipsi in sta in gorišči, potem velja

Zakaj ravno
Ker so ugotovili, da ravno polovica zgornje vsote nastopa tudi v enačbi in s tem sta oba pogleda povezana, kar pa matematike pošlje v neustavljivo vzhičenost.

Enačba elipse

Elipsa je stožnica, predstavnica krivulj drugega reda, saj njena množica ravninskih točk ustreza enačbi druge stopnje Ax² + Bxy + Cy² + Dx + Ey + F = 0

Enačba elipse, ki ima središče v izhodišču koordinatnega sistema in sta in njeni polosi, je enaka

Pri tem najprej predpostavimo, da je , kar pomeni, da je elipsa v dolžino (velika polos a je vodoravna) daljša kot v višino (mala polos b je navpična).
Kaj se zgodi, če je obratno, bomo zapisali nižje spodaj.

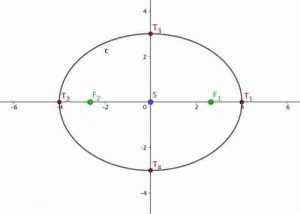
Od tod lahko zapišemo tudi koordinati gorišč in , in sicer in , kjer je .
Število se imenuje linearna ekscentričnost. Zakaj tako ime?
Kdo bi vedel. Bistveno je, da veš, da linearna ekscentričnost  vpliva na sploščenost elipse. Bolj je elipsa sploščena, višja je njena ekscentričnost.
Količnik pa imenujemo numerična ekscentričnost elipse.

Temena elipse so točke .
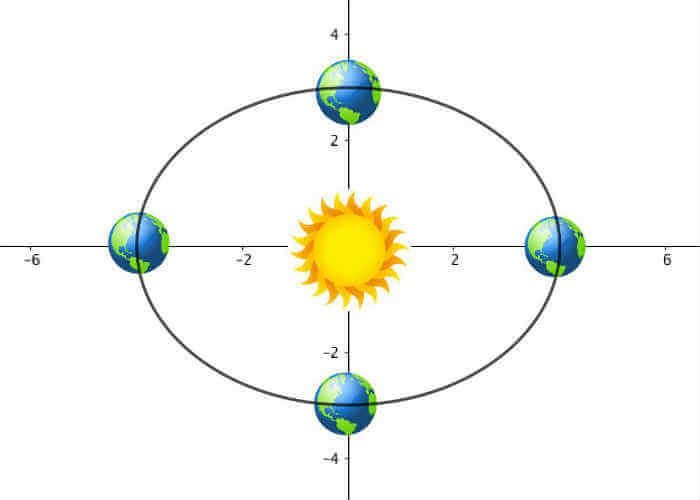
Če imaš rad vesolje, se spomni, da Zemlja potuje okoli sonca po elipsi. Temena elipse so ravno čas enakonočja in solsticija.

Predpostavimo sedaj, da imamo primer, ko je , to pomeni, da je elipsa višja (velika polos b je navpična) od svoje dolžine (mala polos a je vodoravna).
V tem primeru je vse enako, le linearno ekscentričnost izračunamo drugače, in sicer tako, da in zamenjamo, torej .

Če si bolj vizualni tip učenca, si za lažjo predstavo poglej spodnji videoposnetek “Elipsa”.

Povzetek:
Temena elipse:

Gorišča elipse: in , kjer je . To velja za primer, ko je . Če je , izračunamo iz formule .

Zanimivost: Si vedel, da se elipsa pretvori v krožnico, ko je izpolnjen pogoj a=b. Torej, ko sta obe polosi enaki, ekscentričnost pa je 0.

Elipsa v premaknjeni legi

Tako, zdaj vemo vse o elipsi v središčni legi, tj. če je njeno središče v središču koordinatnega sistema. Kaj pa če je elipsa premaknjena?

Enostavno. Premik elipse se v enačbi odraža takole:

Sedaj je središče elipse prestavljeno v točko . Podobno so prestavljena tudi temena in gorišča. Sedaj velja

in

pri čemer se izračuna na enak način kot prej: , če je in , če je .

V spodnjih videih si lahko ogledaš nekaj nalog iz snovi
ELIPSA.

Točki in sta temeni elipse v središčni legi. Zapiši enačbo elipse, koordinate vseh temen in gorišč ter jo nariši.

Iz točk in dobimo polosi in . To je vse, kar potrebujemo, da po formuli izračunamo preostalo.

Elipsa ima enačbo . Zapiši koordnate temen in gorišč ter izračunaj tako da bo točka ležala na elipsi.

Iz formule izpišemo in . To je vse, kar potrebujemo, da izračunamo temena in gorišči. Da bo točka ležala na elipsi, moramo njene koordinate vstaviti v enačbo elipse. Od tod izračunamo .

Če te v zvezi s snovjo elipsa še kaj zanima, ali pa potrebuješ poglobljeno razlago, se oglasi pri nas na inštrukcije za matematiko, kjer ti z veseljem razložimo vse kar te v zvezi s snovjo zanima.